Backward simulation performed with Mercury6 ``A Hybrid Symplectic Integrator that Permits Close Encounters between Massive Bodies''. Monthly Notices of the Royal Astronomical Society, vol 304, pp793-799.
Simulation based on nominal orbital paramters (21st March 2024)
Simulation parameters
)O+_06 Integration parameters (WARNING: Do not delete this line!!)
) Lines beginning with `)' are ignored.
)---------------------------------------------------------------------
) Important integration parameters:
)---------------------------------------------------------------------
algorithm (MVS, BS, BS2, RADAU, HYBRID etc) = BS
start time (days)= 2460309.50000
stop time (days) = -1e8
output interval (days) = 100
timestep (days) = 0.05
accuracy parameter=1.d-12
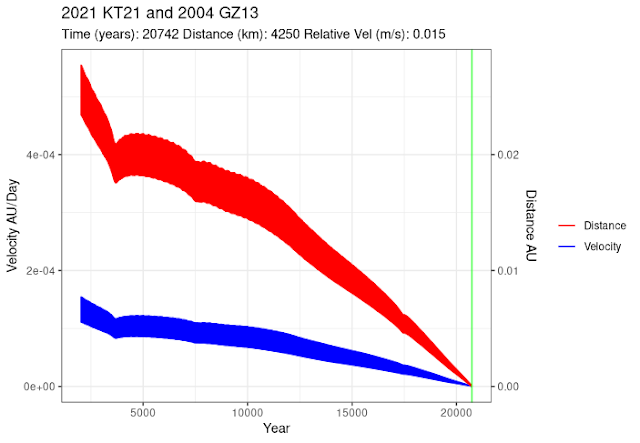
Following a comment from Adrien Coffinet, here is a forward simulation to show that as correctly guessed, the two asteroids might be again in a similar orbital configuration about 20K years from now: